
ディープラーニングネットワークは、音声認識、写真キャプション、言語間のテキスト翻訳において高いパフォーマンスを発揮するように訓練されてきました。ディープラーニングネットワークの実世界問題への応用は広く普及していますが、なぜそれほど効果的なのかという理解は未だに不足しています。統計学におけるサンプルの複雑性や非凸最適化理論に鑑みると、これらの実証的結果はあり得ないはずです。しかしながら、ディープラーニングネットワークの訓練と有効性におけるパラドックスは調査中で、高次元空間の幾何学における知見も得られつつあります。ディープラーニングの数学的理論は、ディープラーニングの機能を明らかにし、様々なネットワークアーキテクチャの長所と短所を評価し、大きな改善につながる可能性があります。ディープラーニングは、人間がデジタルデバイスとコミュニケーションをとる自然な方法を提供し、汎用人工知能(AI)の構築の基盤となっています。ディープラーニングは大脳皮質の構造に着想を得ており、自律性と汎用知能に関する知見は、計画や生存に不可欠な他の脳領域にも見出される可能性がありますが、これらの目標を達成するには大きなブレークスルーが必要となるでしょう。
1884年、エドウィン・アボットは『フラットランド:多次元ロマンス』(1)(図1)を執筆しました。この本はヴィクトリア朝社会への風刺として書かれたものですが、次元が空間に関する私たちの直感をどのように変えるかを探求しているため、今もなお読み継がれています。フラットランドは幾何学的な生き物たちが住む二次元の世界でした。これらの生き物たちは二次元数学を完全に理解しており、円は三角形よりも完璧だと考えていました。この物語の中で、四角い紳士が球体の夢を見て、自分の宇宙が彼やフラットランドの誰もが想像できないほど広大であるかもしれないという可能性に目覚めます。彼は誰にもそれが可能であることを納得させることができず、最終的に投獄されました。

図1 エドウィン・A・アボット著『フラットランド:多次元ロマンス』1884年版の表紙(1)。住民は2次元的な形で表現され、社会における地位は辺の数によって決定されていた。
1次元から2次元へ、そして2次元から3次元へと移行する際に、空間に新たな次元が加わることは容易に想像できます。2次元では線が交差し、3次元では紙が折り重なることさえあります。しかし、3次元の物体が4次元空間で折り重なることは、19世紀にチャールズ・ハワード・ヒントンが成し遂げた概念に匹敵するほどの高度な発想です(2)。さらに高次元の空間にはどのような特性があるのでしょうか?100次元の空間、あるいは100万次元の空間に住むとは、どのような感じでしょうか?あるいは、私たちの脳のように、ニューロン間のシナプスの数である10億×100万次元の空間は、どのような感じでしょうか?
1987年、デンバー・テック・センターで第1回ニューラル情報処理システム(NeurIPS)カンファレンスとワークショップが開催されました(図2)。参加者は600名に上り、物理学、神経科学、心理学、統計学、電気工学、コンピュータサイエンス、コンピュータビジョン、音声認識、ロボティクスなど、幅広い分野から集まりました。しかし、彼らには共通点がありました。彼らは皆、従来の手法では容易に解決できない難解な問題に取り組んでおり、それぞれの専門分野では異端児である傾向がありました。振り返ってみると、33年後、これらのはみ出し者たちは、ビッグデータセットが集積する高次元空間、つまり私たちが現在生きている世界へと、それぞれの分野の最先端を切り開いていました。私は、毎年開催されるNeurIPSカンファレンスを主催する財団の会長として、現代の機械学習を生み出したコミュニティの目覚ましい進化を目の当たりにしてきました。このカンファレンスは着実に成長し、2019年には14,000名を超える参加者を集めました。多くの難解な問題が最終的に解決可能となり、今日では機械学習は現代の人工知能(AI)の基盤となっています。機械学習の初期の目標は、人工知能の目標よりも控えめなものでした。機械学習は、汎用知能を直接目指すのではなく、データからの学習を主要なツールとして、知覚、言語、運動制御、予測、推論といった実用的な問題に取り組むことから始まりました。対照的に、AIにおける初期の試みは、手作業で構築された低次元アルゴリズムを特徴としていました。しかし、このアプローチは、よく制御された環境でのみ機能しました。例えば、Blocks Worldでは、すべてのオブジェクトは直方体で、同じ色で塗装され、照明が固定された環境に置かれていました。これらのアルゴリズムは、オブジェクトが複雑な形状を持ち、反射率が広範囲に変化し、照明条件が制御されていない現実世界の視覚には対応していませんでした。現実世界は高次元であり、それに適合できる低次元モデルは存在しない可能性があります(3)。同様の問題は、意味の複雑さを無視した記号と構文に基づく初期の自然言語モデルでも発生しました(4)。深層学習言語モデルの複雑さが現実世界の複雑さに近づくと、実用的な自然言語アプリケーションが可能になりました。数百万のパラメータを持ち、数百万のラベル付き例で学習された自然言語モデルは、今や日常的に使用されています。さらに大規模なディープラーニング言語ネットワークは、導入からわずか10年足らずで運用が開始され、数百万人のオンラインユーザーにサービスを提供しています。

図2. ニューラル情報処理システム会議には、科学と工学の様々な分野の研究者が集まりました。第1回会議は1987年にデンバー・テックセンターで開催され、それ以来毎年開催されています。最初の数回の会議は、IEEE情報理論学会の主催でした。
ディープラーニングの起源 私は『ディープラーニング革命:人工知能と人間の知能の出会い』(5)という本を執筆しました。この本では、ディープラーニングがどのように誕生したかを説明しています。ディープラーニングは、脳に見られる超並列アーキテクチャにヒントを得たもので、その起源は1950年代のフランク・ローゼンブラットによるパーセプトロン(6)に遡ります。パーセプトロンは、マカロックとピッツ(7)が導入した単一ニューロンの簡略化モデルをベースとしていました。パーセプトロンはパターン認識を行い、ラベル付きの例を分類することを学習しました(図3)。ローゼンブラットは、新しい入力を正しく分類できるパラメータのセットがあり、十分な例がある場合、彼の学習アルゴリズムは必ずそれを見つけるという定理を証明しました。この学習アルゴリズムは、ラベル付きデータを使用して、バイナリしきい値ユニットへの入力の重みであるパラメータに小さな変更を加え、勾配降下法を実装しました。このシンプルなパラダイムは、今日のより大規模で洗練されたニューラルネットワークアーキテクチャの中核を成していますが、パーセプトロンからディープラーニングへの移行はスムーズなものではありませんでした。その経緯から学ぶべき教訓があります。

図3 初期のパーセプトロンは大規模なアナログシステムでした (4)。(上) 視覚入力を受け取るアナログ パーセプトロン コンピュータ。ラックにはポテンショメータがあり、モーターで駆動され、その抵抗はパーセプトロン学習アルゴリズムによって制御されます。(出典: 文献 6)。(右) 1958 年 7 月 8 日付の New York Times の記事、UPI 通信社の報道より。パーセプトロン マシンは 1959 年の完成時に 10 万ドル、現在の価値で約 100 万ドルの費用がかかると予想されていました。1958 年に 200 万ドル、現在の価値で 2,000 万ドルの費用がかかった IBM 704 コンピュータは 1 秒あたり 12,000 回の乗算を実行でき、当時としては驚異的な速度でした。はるかに安価な Samsung Galaxy S6は 1 秒あたり 340 億回の演算を実行でき、その 100 万倍以上も高速です。
パーセプトロン学習アルゴリズムは実数を使った計算を必要としましたが、1950年代のデジタルコンピュータでは効率的に実行できませんでした。 ローゼンブラットは海軍研究局から現在の 100 万ドルに相当する助成金を受け、可変の重みを表す一連のモーター駆動式ポテンショメータを使用して重みの更新を並列に実行できる大型アナログ コンピュータを構築しました (図 3)。マスコミの大きな期待 (図 3) は、マービン ミンスキー氏とシーモア パパート氏によって打ち砕かれました。彼らは、著書「パーセプトロン」(8) で、パーセプトロンは重み空間で線形に分離可能なカテゴリのみを表現できることを示しました。著書の最後で、ミンスキー氏とパパート氏は単層パーセプトロンを多層パーセプトロンに一般化し、1 つの層が次の層に情報を入力する可能性を検討しましたが、これらのより強力な多層パーセプトロンをトレーニングする方法があるかどうかは疑問でした。残念ながら、多くの人がこの疑問を決定的なものと受け止め、1980 年代に新世代のニューラル ネットワーク研究者がこの問題を新たに検討するまで、この分野は放棄されていました。
1960 年代に研究に利用できた計算能力は、今日と比較すると微々たるもので、学習よりもプログラミングが重視され、おもちゃの問題を解くプログラムを書くという初期の進歩は有望に見えました。1970 年代までには学習は人気を失いましたが、1980 年代までにはデジタル コンピュータの速度が向上し、中規模のニューラル ネットワークをシミュレートできるようになりました。その後の 1980 年代のニューラル ネットワーク復活の時期に、ジェフリー ヒントンと私はボルツマン マシンの学習アルゴリズムを導入し、一般の認識に反して多層ネットワークをトレーニングできることを証明しました (9)。ボルツマン マシンの学習アルゴリズムは局所的で、単一ニューロンの入力と出力の相関、つまり皮質に見られるヘブ可塑性の一形態 (10) のみに依存します。興味深いことに、トレーニング中に計算された相関は、自己参照学習を防ぐために、入力がない場合に発生する相関、つまりスリープ状態と呼んでいるものによって正規化される必要があります。ラベルなしの入力の結合確率分布を教師なし学習モードで学習することも可能です。しかし、ほぼ同時期に導入された、誤差のバックプロパゲーションに基づく別の学習アルゴリズムは、局所性を犠牲にするものの、はるかに効率的でした(11)。これらの学習アルゴリズムはどちらも、損失関数を最小化するためにパラメータ値を段階的に変更する最適化手法である確率的勾配降下法を用いています。通常、これは少数の訓練例の勾配を平均化した後に行われます。
パラメータ空間の迷宮 1980年代のネットワークモデルは、入力と出力の間に2層以上の隠れユニットを持つことは稀でしたが、統計学習の基準からすると既に過剰パラメータ化されていました。実証研究により、当時は説明できなかった多くのパラドックスが明らかになりました。当時のネットワークは今日の基準からすると非常に小さいものでしたが、従来の統計モデルよりも桁違いに多くのパラメータを持っていました。統計学の定理の限界によれば、当時利用可能な比較的小規模な訓練データでは一般化は不可能であるはずです。しかし、重み減衰などの単純な正則化手法でさえ、驚くほど優れた一般化を示すモデルを生み出しました。
さらに驚くべきことに、非凸損失関数の確率的勾配降下法は、局所最小値に陥ることはほとんどありませんでした。下降途中には、誤差がほとんど変化しない長いプラトーがあり、その後急激に低下しました。これらのネットワーク モデルとその高次元パラメータ空間の幾何学的形状により、従来の直感によって予測された失敗とは対照的に、効率的にソリューションに到達し、優れた一般化を達成することができました。
ネットワークモデルは、入力空間を出力空間にマッピングする方法を学習する高次元動的システムです。これらの関数は、私たちがようやく理解し始めた特別な数学的特性を持っています。高次元パラメータ空間では、ほとんどの臨界点が鞍点(12)であるため、学習中に局所的最小値が生じることは稀です。確率的勾配降下法によって優れた解が容易に見つかるもう一つの理由は、唯一の解を求める低次元モデルとは異なり、優れた性能を持つ様々なネットワークがパラメータ空間内のランダムな開始点から収束していくことです。過剰パラメータ化(13)により、解の退化により、問題の本質は干し草の山から針を探す問題から、針の山の干し草の山へと変化します。
多くの疑問が未解決のまま残されています。なぜこれほど少ない例数とこれほど多くのパラメータから一般化が可能なのでしょうか?なぜ確率的勾配降下法は他の最適化手法と比較して、有用な関数を見つけるのに非常に効果的なのでしょうか?問題に対するすべての良い解の集合はどれくらいの大きさなのでしょうか?良い解は互いに何らかの形で関連しているのでしょうか?一般化を向上させることができるアーキテクチャ特性と帰納的バイアスとの間にはどのような関係があるのでしょうか?これらの疑問への答えは、より優れたネットワークアーキテクチャとより効率的な学習アルゴリズムを設計する上で役立つでしょう。
1980年代には、ニューラルネットワークの学習アルゴリズムがネットワーク内のユニット数と重みの数に応じてどれほどスケールするかは誰も知りませんでした。多くのAIアルゴリズムが組み合わせ的にスケールするのとは異なり、ディープラーニングネットワークは、ネットワークの規模が拡大しても、学習はパラメータ数に比例してスケールし、層が追加されるにつれて性能が向上し続けました(14)。さらに、ディープラーニングネットワークの超並列アーキテクチャは、マルチコアチップによって効率的に実装できます。完全並列ハードウェアを用いた学習と推論の計算量はO(1)です。これは、好ましい計算特性が同時に実現される稀有な例です。
新しい種類の関数が導入されると、それを完全に探求するには何世代もかかります。例えば、ジョゼフ・フーリエが1807年にフーリエ級数を導入した際、彼は収束を証明できず、関数としての地位が疑問視されました。しかし、技術者たちはフーリエ級数を用いて熱方程式を解き、他の実用的な問題にも応用しました。この種類の関数の研究は、最終的に数学の至宝とも言える関数解析への深い洞察へとつながりました。
ディープラーニングの本質 今日展開されているニューラルネットワークアーキテクチャ探究の第三波は、1950年代のパーセプトロン、そして1980年代の多層ニューラルネットワークに端を発した最初の二つの波に続き、学術的な起源を大きく超えて発展してきました。マスコミはディープラーニングをAIと呼び直しています。ディープラーニングがAIにもたらしたのは、それを現実世界に根付かせたことです。現実世界はアナログで、ノイズが多く、不確実で、高次元であり、従来のAIにおける記号とルールの白黒の世界とは決して調和しませんでした。ディープラーニングは、これら二つの世界をつなぐインターフェースを提供します。例えば、自然言語処理は従来、記号処理の問題として捉えられてきました。しかし、リカレントニューラルネットワークにおける言語翻訳のエンドツーエンド学習は、文から統語情報と意味情報の両方を抽出します。自然言語アプリケーションは、多くの場合、記号ではなく、文中の次の単語を予測するように訓練された深層学習ネットワークにおける単語埋め込みから始まります(15)。これは意味的に深く、単語間の関係性だけでなく連想も表します。かつては「単なる統計」と考えられていた深層再帰型ネットワークは、脳内の電気活動のように情報が流れる高次元の動的システムです。
1960年代の人工知能研究における初期の緊張関係の一つは、人間の知能との関係でした。人工知能の工学的目標は、直感に基づいたプログラムを作成することで人間の知能の機能的能力を再現することでした。私はかつて、カーネギーメロン大学のコンピュータ科学者であり、1956年の画期的なダートマス夏季会議に出席した人工知能の先駆者の一人であるアレン・ニューウェルに、なぜAIの先駆者たちは人間の知能の基盤である脳を無視してきたのかと尋ねました。脳の性能は、AIにおけるあらゆる難問が解決可能であることを示す唯一の存在証明でした。彼は私に、個人的には脳研究からの洞察に前向きだったが、当時は脳について十分な知識がなかったため、あまり役に立たなかったと語りました。
時が経つにつれ、AI 業界における考え方は「十分にわかっていない」から「脳は関係ない」へと変化しました。この考え方は、航空との類推によって一般的に正当化されました。「飛行機を作りたいのなら、羽ばたく鳥やその羽毛の特性を研究するのは時間の無駄だ」というものです。しかし、それとはまったく逆に、ライト兄弟は、飛行効率の高い滑空鳥を熱心に観察していました (16)。彼らが鳥から学んだのは、実用的な翼の設計アイデアと空気力学の基本原理でした。現代のジェット機は翼の先端にウィングレットを取り付けて、燃料を 5% 節約するとともに、ワシの翼端によく似ています (図 4)。脳が感覚情報を処理し、証拠を蓄積し、意思決定を行い、将来の行動を計画する方法については、現在でははるかに多くのことが分かっています。ディープラーニングも同様に自然界からヒントを得ています。コンピュータサイエンスにおいて、アルゴリズム生物学と呼ばれる新たな分野が急成長を遂げています。これは、生物システムが用いる幅広い問題解決戦略を記述しようとするものです(17)。ここでの教訓は、進化によって磨かれ、生命の連鎖を通じて人類に受け継がれてきた、複雑な問題に対する一般原理と具体的な解決策を、自然から学ぶことができるということです。

図4. 自然はエネルギー効率を高めるために鳥類を最適化しました。(A) ワシの翼端の湾曲した羽毛は滑空時のエネルギー効率を高めます。(B) 民間ジェット機のウィングレットは渦の抗力を低減することで燃料を節約します。
現実のニューロンの複雑さと、ニューラルネットワークモデルにおけるモデルニューロンの単純さの間には、際立った対照があります。ニューロン自体は、内部時間スケールが広範囲にわたる複雑な動的システムです。現実のニューロンの複雑さの多くは細胞生物学、すなわち各細胞が自らエネルギーを生成し、様々な困難な条件下で恒常性を維持する必要性から受け継がれています。しかし、ニューロンの他の特徴も計算機能にとって重要である可能性が高く、その一部はモデルネットワークではまだ活用されていません。これらの特徴には、特定の機能に最適化された多様な細胞タイプ、数秒単位の時間スケールで促進または抑制する可能性のある短期シナプス可塑性、数秒から数時間に及ぶ入力履歴によって制御されるシナプス内部可塑性を支える生化学反応のカスケード、脳がオフラインになり自己再構築を行う睡眠状態、そして脳領域間のトラフィックを制御する通信ネットワーク(18)が含まれます。脳とAIの相乗効果は、生物学と工学の両方に利益をもたらす可能性があります。
大脳新皮質は2億年前に哺乳類に出現しました。大脳新皮質は脳の外側にある折り畳まれたニューロンのシートで、灰白質と呼ばれます。ヒトでは、平らにすると直径約30cm、厚さ約5mmです。約300億個の皮質ニューロンが6層に層状に存在し、局所的な定型パターンで互いに高度に相互接続されています。大脳新皮質は進化の過程で脳の中心核に比べて大きく拡大し、特にヒトでは脳容積の80%を占めています。この拡大は、体の大きさに比べて拡大していないほとんどの脳領域とは異なり、大脳皮質の構造がスケーラブル(多ければ多いほど良い)であることを示唆しています。興味深いことに、大脳皮質の白質を形成する局所的な接続に比べて長距離接続ははるかに少ないですが、その体積は灰白質の体積の5/4乗に比例して拡大し、大きな脳では灰白質の体積よりも大きくなります(19)。脳構造のスケーリング則は、重要な計算原理に関する洞察をもたらす可能性があります(20)。細胞の種類やそれらの接続性を含む皮質構造は皮質全体で共通しており、異なる認知システムに特化した領域が存在します。例えば、視覚皮質は視覚に特化した回路を進化させており、これは最も成功した深層学習アーキテクチャである畳み込みニューラルネットワーク(CNN)で活用されています。大脳新皮質は汎用的な学習アーキテクチャを進化させ、多くの特殊用途の皮質下構造の性能を大幅に向上させています。
脳は、空間的に構造化された計算コンポーネントを11桁も備えています(図5)。シナプスレベルでは、大脳皮質の1立方ミリメートル(米粒ほどの大きさ)あたりに10億個のシナプスが存在します。現在、最大規模の深層学習ネットワークは、10億個の重みに達しています。皮質は、それぞれが特定の問題の解決に特化した数十万個の深層学習ネットワークに匹敵する処理能力を備えています。これらのエキスパートネットワークはどのように構成されているのでしょうか?ネットワークレベルより上位の調査レベルでは、異なる皮質領域間の情報の流れを体系化します。これはシステムレベルの通信問題です。皮質における全体的な情報の流れがどのように管理されているかを研究することで、数千もの特殊化されたネットワークをどのように体系化するかについて多くの知見が得られます。皮質内の長距離接続は、長距離情報送信に必要なエネルギー需要と、大きな空間を占めるという両方の理由から、コストが高いため、まばらです。スイッチングネットワークは、感覚領域と運動領域の間で情報をルーティングし、進行中の認知要求に応じて迅速に再構成することができます(18)。
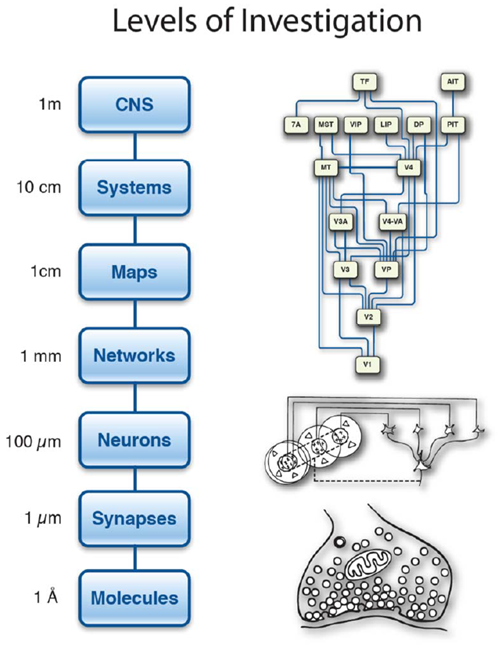
図5. 脳の探究レベル。エネルギー効率は、シナプスにおける少数の分子によるシグナル伝達によって達成される。脳内のニューロン間の相互接続は3次元的である。接続性は局所的には高いが、離れた皮質領域間では比較的疎である。皮質の組織化原理は、階層構造をなす複数の感覚表面および運動表面マップに基づいている。皮質は多くの皮質下領域と連携して、行動を生み出す中枢神経系(CNS)を形成する(『計算脳』(Churchland, P. and Sejnowski, T., MIT Press, 1992)より引用)。
次世代 AI システムの構築におけるもう 1 つの大きな課題は、ディープラーニング専門家ネットワークの高度に異種混合なシステムのメモリ管理です。学習済みの記憶を劣化させることなく、これらのネットワークを柔軟に更新する必要があります。これが、安定した生涯学習を維持する問題です (21)。 サブシステム間のメモリ損失と干渉を最小限に抑える方法はいくつかあります。 1 つの方法は、新しい経験を保存する場所を選択することです。これは、皮質が全体的に一貫した電気活動パターンに入る睡眠中に発生します。睡眠紡錘波と呼ばれる短い振動イベントは、夜間に何千回も繰り返され、記憶の統合に関連しています。紡錘波は、日中に経験した最近のエピソードの再生によって引き起こされ、長期的な皮質意味記憶に慎重に統合されます (22, 23)。
ディープラーニングの未来 今日のディープラーニングへの焦点は大脳皮質に着想を得たものですが、運動や生命維持機能を制御するには、はるかに幅広いアーキテクチャが必要です。哺乳類の脳の生存に不可欠な皮質下領域は、強化学習を担う基底核や、脳に運動指令の順モデルを提供する小脳など、すべての脊椎動物に存在します。ヒトは超社会的であり、複雑な社会的相互作用を支えるために、広範な皮質および皮質下神経回路を有しています(24)。これらの脳領域は、自律型AIシステムの構築を目指す人々にインスピレーションを与えるでしょう。
例えば、脳幹のドーパミンニューロンは報酬予測誤差を計算しますが、これは強化学習における時間的差分学習アルゴリズムの重要な計算であり、ディープラーニングと組み合わせることで、2017年にAlphaGoが囲碁の世界チャンピオンである柯潔を破ることを可能にしました(25)。皮質と基底核全体に拡散投射する中脳のドーパミンニューロンからの記録は、シナプス可塑性を調節し、長期報酬を得るための動機付けを提供します(26)。その後、ヒトにおけるドーパミンニューロンの役割が確認され、神経経済学という新しい分野が生まれ、その目的は、ヒトがどのように経済的決定を下すのかについてより深く理解することです(27)。他のいくつかの神経調節システムも、負の報酬、驚き、自信、時間的割引を表す行動を導くために脳全体の状態を制御します(28)。
運動システムは、生物学に着想を得たソリューションが役立つ可能性がある AI のもう 1 つの領域です。動物の滑らかな動きと、ほとんどのロボットの剛体動作を比較してください。重要な違いは、すべての動物の高次元筋肉組織の制御に見られる並外れた柔軟性です。高次元運動計画空間における協調行動は、ディープラーニング ネットワーク (29) で活発に研究されている領域です。脊髄、脳幹、前脳の複数の制御層がどのように協調しているかを説明するために、分散制御の理論も必要とされています。脳と制御システムはどちらも、不安定になる可能性があるフィードバック ループの時間遅延に対処する必要があります。小脳にある体の順方向モデルは、運動コマンドの感覚結果を予測する方法を提供し、感覚予測誤差を使用してオープン ループ制御が最適化されます。たとえば、前庭眼反射 (VOR) は、オープン ループで頭部加速度信号を迅速に使用することで、頭部の動きに関係なく網膜上の画像を安定させます。 VORのゲインは網膜からのスリップ信号によって調整され、小脳はこれを用いてスリップを低減します(30)。脳は感覚神経と運動神経の帯域幅が限られているため、更なる制約を受けますが、速度と精度のトレードオフが多様なコンポーネントで構成される階層型制御システムによって、これらの制約を克服することができます(31)。同様の多様性は工学システムにも存在し、不完全なコンポーネントを持ちながらも高速かつ正確な制御を可能にします(32)。
汎用人工知能に向けて ディープラーニングの最新技術から汎用人工知能への道筋はあるのだろうか?進化の観点から見ると、ほとんどの動物はそれぞれのニッチで生き残るために必要な問題を解決できるが、一般的な抽象推論は比較的最近になって人類の系統に出現した。しかし、人間は抽象推論が得意ではなく、論理的に推論する能力を身につけるには長い訓練が必要である。これは、論理的に最適化されていない論理的ステップをシミュレートするために脳システムを使用しているためである。小学生は単純な算数を習得するために何年もかけて学習し、1秒クロックのデジタルコンピュータを事実上エミュレートしている。とはいえ、人間の推論能力は、合理的な計画と意思決定のためのディープラーニングネットワークの大規模システムを進化させることが可能であるという原理的な証明である。しかし、DeepMindがコピー、ソート、ナビゲーションを学習するために開発したニューラルチューリングマシン(33)のような、ハイブリッドなソリューションも実現可能かもしれない。オルゲルの第二法則によれば、自然は人間よりも賢いが、それでも改善の余地がある。
近年、ディープネットワークにおける教師あり学習の成功により、大規模データセットを利用できるアプリケーションが急増しています。言語翻訳は、大規模な翻訳テキストコーパスを用いたトレーニングによって大幅に改善されました。しかし、大規模なラベル付きデータセットが利用できないアプリケーションも数多く存在します。人間は一般的に、現実世界における結果について無意識のうちに予測を行い、予期せぬ出来事に驚かされます。他のデータストリームから将来の出力を予測することを学習目標とする自己教師学習は、有望な方向性です (34)。模倣学習もまた、重要な行動を学習し、世界に関する知識を獲得するための強力な方法です (35)。人間には学習方法が数多くあり、成人レベルのパフォーマンスを達成するには長い発達期間が必要です。
脳は、問題に対するアイデアや解決策を知的かつ自発的に生み出します。被験者が脳スキャナー内で静かに横たわるように指示されると、活動は感覚運動領域から、無意識の活動を含む内面の思考をサポートする領域のデフォルトモードネットワークに切り替わります。生成ニューラルネットワークモデルは、豊富な生の感覚データから結合確率分布を学習することを目的として、教師なしで学習できます。ボルツマンマシンは生成モデルの例です (9)。ボルツマンマシンが入力を分類するようにトレーニングされた後、出力ユニットをオンにすると、入力層でそのカテゴリからの一連の例が生成されます (36)。生成敵対ネットワーク(GAN)は、自己教師学習によって学習した確率分布から新しいサンプルを生成することもできます (37)。脳はまた、夢を見ている睡眠中に鮮明な視覚イメージを生成しますが、それはしばしば奇妙です。
未来を見据えて 私たちは今、情報の時代とも言える新たな時代の幕開けを迎えています。センサーからデータが噴出しており、データはパイプラインの源泉となっています。パイプラインはデータを情報へ、情報を知識へ、知識を理解へ、そして運が良ければ知識を知恵へと変えていきます。私たちは現実世界における複雑で高次元の問題への取り組みに向けて、最初の一歩を踏み出しました。赤ちゃんのように、歩みを進めるというよりはよろめきながらの歩みですが、重要なのは、私たちが正しい方向に向かっているということです。ディープラーニング・ネットワークは、デジタルコンピュータと現実世界をつなぐ架け橋であり、これにより私たちは自分のペースでコンピュータとコミュニケーションをとることができます。私たちは既にスマートスピーカーと会話をしていますが、スマートスピーカーはさらに賢くなるでしょう。キーボードは時代遅れとなり、タイプライターと共に博物館に展示されるでしょう。こうしてディープラーニングの恩恵は誰もが享受できるようになります。
ユージン・ウィグナーは「自然科学における数学の不合理な有効性」というエッセイの中で、物理理論の数学的構造がしばしばその理論への深い洞察を明らかにし、それが経験的予測につながることに驚嘆しました(38)。また注目すべきは、方程式に含まれる物理定数と呼ばれるパラメータが非常に少ないことです。本稿のタイトルはウィグナーの考えを反映しています。しかし、物理法則とは異なり、ディープラーニングネットワークには豊富なパラメータが存在し、それらは可変です。私たちは、非常に高次元な空間における表現と最適化の探究を始めたばかりです。おそらくいつの日か、ディープラーニングネットワークの構造解析が理論的な予測につながり、知性の本質に関する深い洞察が明らかになるでしょう。私たちは次元性の恩恵を受けることができるのです。
世界における信号の複雑さを記述する関数のクラスが一つ見つかった今、他にもあるかもしれない。もしかしたら、高次元空間には、私たちがまだ探求していない超並列アルゴリズムの宇宙が存在するのかもしれない。それは、私たちが住む三次元世界やデジタルコンピュータにおける一次元的な命令列からの直感を超越する。フラットランドの紳士の四角形(図1)やフラマリオンの彫刻に登場する探検家(図6)のように、私たちは古い地平線をはるかに超えた新たな世界を垣間見たのかもしれない。

図6. カミーユ・フラマリオンの1888年の著書『大気:民衆気象学』(L'atmosphère: météorologie populaire、パリ、アシェット社、163ページ)の版画。フラマリオンの本の版画に添えられたキャプションは次の通り。「中世のある宣教師は、天と地が接する点を発見したと語っている…」